Diagnostics

What is homoscedasticity? Why does it matter? How can we see if it appears to be satisfied?

What is the assumption of linearity? Why does it matter? How can we see if it appears to be satisfied?

Why are outliers overly influential in a regression analysis?

What is a studentized residual? A studentized deleted residual?

What is leverage?

What are dfbetas?

Concepts

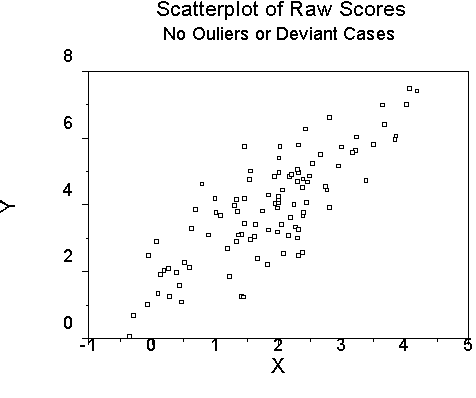
Is the regression line a good representation of the data? It will be if the data are bivariate or multivariate normal. But often, real data are not so distributed.

  1. Residual plots - examine residual plots for evidence of nonlinearity and heteroscedasticity.

 

 

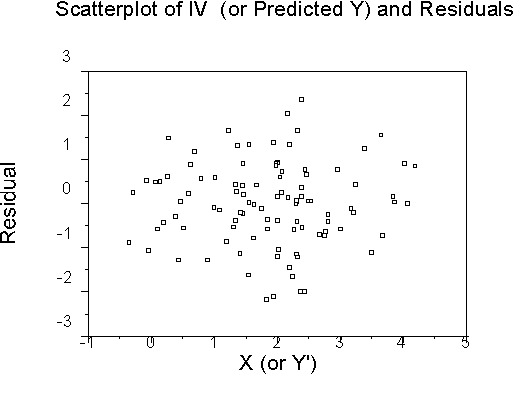
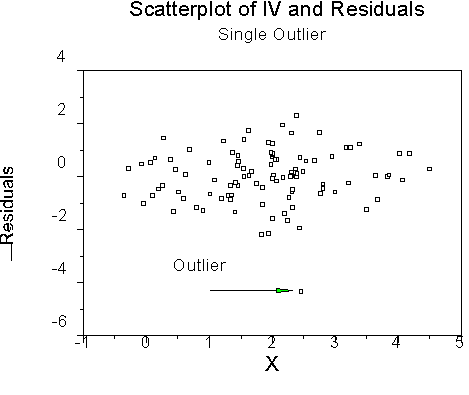
Outliers - deviant cases. Detected by analyzing residuals.

 

Standardized residuals ZRESID: ZRESID=(Y-Y')/Sy.x or e/Sy.x. The residual divided by the standard deviation of residuals. The mean of the residuals is zero. The SD is also known as the standard error of prediction.

Look for large values (some say |zresid|>2).

 

Studentized Residual SRESID:

 

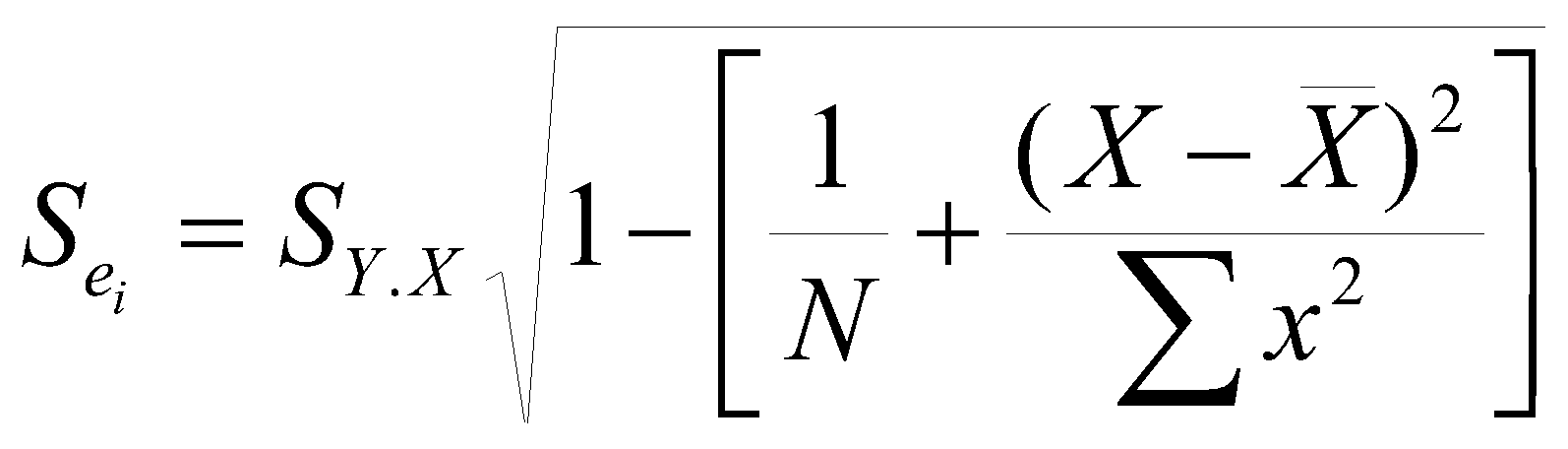
The studentized residual recognizes that the error associated with predicting values far from the mean of X is larger than the error associated with predicting values closer to the mean of X. The studentized residual boosts the size of residuals for points distant from the mean of X. Again, look for large values. [The SAS manual portion of the course shows you how to compute approximate confidence limits for this residual, and also for the studentized deleted residual, shown next.]

 

Studentized Deleted Residuals (SDRESID):

 

Same as the studentized residual, but the regression equation is recalculated with the set of data excluding the observation in question. The equation is used to predict Y for the observation in question, and the residual is calculated. After that, it's an ordinary studentized residual. Again, look for large values.

 

Influence Analysis.

Helps you examine how observations control the regression equation. 

Leverage:

 

 

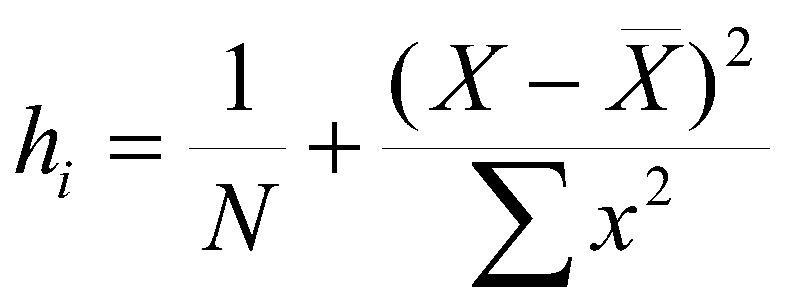
An index of the importance (leverage) of an observation for the regression equation.

 

  1. Function solely of X
  2. Large deviation of X has large leverage.
  3. Max value of 1.
  4. Average value of (k+1)/N, where k is the number of independent variables.

 

DFBETA and standardized DFBETA. These indices show how much the slope or intercept change if you delete the ith person; they allow for both X and Y.