Partial and Semipartial Correlation
Give a concrete example (names of variables, context) in which it makes sense to compute a partial correlation. Why a partial rather than a semipartial?
Give a concrete example (names of variables, context) in which it makes sense to compute a semipartial correlation. Why a semipartial rather than a partial?
Why is the squared semipartial always less than or equal to the partial correlation?
Why is regression more closely related to the semipartial than the partial correlation?
Describe how you would go about computing a third order partial correlation.
Partial and Semipartial Correlation
Regression tends to be a lot more complicated and difficult than ANOVA. The difficulty comes because there are so many concepts in regression and correlation. The excessive number of concepts comes because the problems we tackle are so messy. With ANOVA, you assign people to treatments, and all sorts of explanations of the results (that is, the associations or correlations between the IVs and DV) get ruled out. With nonexperimental data, we cannot assign people to treatments for practical or ethical reasons. People are always interested in the difference between men & women but we really can't assign people to those groups.
Partial Correlation
We measure individual differences in many things, including cognitive ability, personality, interests & motives, attitudes, and so forth. Many times, we want to know about the influence of one IV on a DV, but one or more other IVs pose an alternative explanation. We would like to hold some third variable constant while examining the relations between X and Y. With assignment we can do this by design. With measures of individual differences, we can do this statistically rather than by manipulation.
The basic idea in partial and semipartial correlation is to examine the correlations among residuals (errors of prediction). If we regress variable X on variable Z, then subtract X' from X, we have a residual e. This e will be uncorrelated with Z, so any correlation X shares with another variable Y cannot be due to Z.
Example
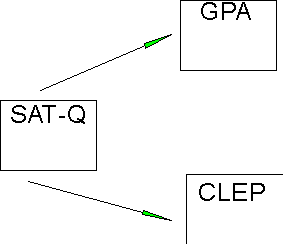
There is at present a debate among educators and policy makers about the use of aptitude and achievement tests as part of college admissions. Some say aptitude tests should be used because they are minimally influenced by formal education. Thus, they tend to level the playing field and account for differences among schools in grade inflation. Other say that achievement tests should be used because they show what people actually know or can do, and they would provide motivation for students to progress beyond basics. There are many complicated arguments that have some merit on both sides. Let's set all that to one side for a moment and think about the utility of such measures for a moment. Suppose what we want to do is to make good admissions decisions in the sense that we want to maximize our prediction of achievement in college from what we know from the end of high school in the area of mathematics. Suppose admit people to college without looking at the data, which are test scores for people on the SAT-Q (quantitative or math aptitude), and scores on a math CLEP test (math achievement) and we look at grades in the standard first year math sequence (differential and integral calculus). We want to know about the prediction of math grades from the two tests.
Our data might look like this:
|
Person |
SAT-Q |
CLEP |
Math GPA |
|
1 |
500 |
30 |
2.8 |
|
2 |
550 |
32 |
3.0 |
|
3 |
450 |
28 |
2.9 |
|
4 |
400 |
25 |
2.8 |
|
5 |
600 |
32 |
3.3 |
|
6 |
650 |
38 |
3.3 |
|
7 |
700 |
39 |
3.5 |
|
8 |
550 |
38 |
3.7 |
|
9 |
650 |
35 |
3.4 |
|
10 |
550 |
31 |
2.9 |
The correlations among our three variables are as follows:
|
|
SAT-Q |
CLEP |
GPA |
|
SAT-Q |
1 |
|
|
|
CLEP |
.87 |
1 |
|
|
GPA |
.72 |
.88 |
1 |
Clearly, both our tests are related to college math mastery as indicated by GPA.
Suppose we regress GPA on SAT-Q. Our regression equation is GPA' = 1.78+.002SATQ and R-square is .52.
If we print our variables, predicted values and residuals, we get:
|
Person |
SAT-Q |
Math GPA |
Pred |
Resid |
|
1 |
500 |
2.8 |
3.01266 |
-0.21266 |
|
2 |
550 |
3.0 |
3.13544 |
-0.13544 |
|
3 |
450 |
2.9 |
2.88987 |
0.01013 |
|
4 |
400 |
2.8 |
2.76709 |
0.03291 |
|
5 |
600 |
3.3 |
3.25823 |
0.04177 |
|
6 |
650 |
3.3 |
3.38101 |
-0.08101 |
|
7 |
700 |
3.5 |
3.50380 |
-0.00380 |
|
8 |
550 |
3.7 |
3.13544 |
0.56456 |
|
9 |
650 |
3.4 |
3.38101 |
0.01899 |
|
10 |
550 |
2.9 |
3.13544 |
-0.23544 |
If we compute the correlations among these variables, we find
|
|
SATQ |
GPA |
PRED |
RESID |
|
SATQ |
1 |
|
|
|
|
GPA |
.72 |
1 |
|
|
|
PRED |
1.0 |
.72 |
1 |
|
|
RESID |
0 |
.69 |
0 |
1 |
Note that SAT and GPA are still correlated .72. SAT and PRED are correlated 1.0. After all, PRED is a linear function of SAT (i.e., a linear transformation of the form Y'=1.78+.002SAT). Especially note that RESID is uncorrelated with SATQ, that is, the correlation between PRED and RESID is zero. Of course, the correlation of SAT and RESID is also zero. Remember that the linear model says that the variance in Y is due in part to X and in part to error. The part due to X is a linear function of X that is perfectly correlated with X. What ever is left (the residual) is what is left when the part due to X is subtracted out. Therefore, the residual must be uncorrelated with X. Recall your Venn Diagrams. Just because the residual is uncorrelated with X doesn't mean it cannot correlated with other things. Note that the residual is correlated .69 with GPA. In our case, you might say that the residual is that part of GPA which is left when SAT is taken out. OK, go ahead and say it!
Now we could also do the same thing predicting GPA from math achievement, our CLEP score. If we do that, we find that GPA'=1.17+.06CLEP and R-square =.77. The correlations among these variables are:
|
|
CLEP |
GPA |
PRED |
RESID |
|
CLEP |
1 |
|
|
|
|
GPA |
.88 |
1 |
|
|
|
PRED |
1.0 |
.88 |
1 |
|
|
RESID |
0 |
.48 |
0 |
1 |
Note that the correlation between CLEP and GPA is larger than for SAT and GPA. Also note that the correlation between the residual and GPA is smaller. But again the predicted values correlate perfectly with the IV and the residuals do not correlate with the IV or predicted values.
One other thing that we could do help determine a pragmatic argument is to regress GPA on both SAT and CLEP at the same time to see what happens. If we do that, we find that R-square for the model is .78, F = 12.25, p < .01. The intercept and b weight for CLEP are both significant, but the b weight for SAT is not significant. The values are
Intercept = 1.16, t=2.844, p < .05
CLEP = 0.07, t=2.874, p < .05
SATQ = -.0007, t=-0.558, n.s.
In this case, we would conclude that the significant unique predictor is CLEP. Although SAT is highly correlated with GPA, it adds nothing to the prediction equation once the CLEP score is entered. (These data are fictional and the sample size is much too small to run this analysis. It's there for illustration only.)
Now suppose we wanted to argue something a little different. Suppose we had a theory that said that all measures of math achievement share a common explanation, which is math ability. In other words, the reason that various (all) math achievement tests are correlated is that they share the math ability factor. In other words, math ability explains the correlation between achievement tests. In path diagram form, we might represent this something like this:

Now it may not be immediately obvious, but this diagram says that there is only one common cause of GPA and CLEP, which is SATQ. This implies that the correlation between GPA and CLEP is due solely to SATQ. If there were other theoretical explanations (e.g., motivation), then these should be drawn into the diagram. As it is, this says that the correlation between GPA and CLEP would be zero except for the shared influence of SATQ.
We have already found the residual of GPA when we regressed GPA on SATQ. We know that this residual is not correlated with SATQ. We can run another regression where we predict CLEP from SATQ. If we do this, we find that CLEP' = 8.57+.04SATQ. R-square is .76. We can also see the values of the variables:
|
Person |
SAT-Q |
CLEP |
Pred |
Resid |
|
1 |
500 |
30 |
30.2025 |
-.20253 |
|
2 |
550 |
32 |
32.3671 |
-.36709 |
|
3 |
450 |
28 |
28.0380 |
-.03797 |
|
4 |
400 |
25 |
25.8734 |
-.87342 |
|
5 |
600 |
32 |
34.5313 |
-2.53165 |
|
6 |
650 |
38 |
36.6952 |
1.30380 |
|
7 |
700 |
39 |
38.8608 |
0.13924 |
|
8 |
550 |
38 |
32.3671 |
5.63291 |
|
9 |
650 |
35 |
36.6962 |
-1.69620 |
|
10 |
550 |
31 |
32.3671 |
-1.36709 |
The correlations among these variables are
|
|
SAT |
CLEP |
PRED |
RESID |
|
SAT |
1 |
|
|
|
|
CLEP |
.87 |
1 |
|
|
|
PRED |
1.0 |
.87 |
1 |
|
|
RESID |
0 |
.49 |
0 |
1 |
Note that the residuals are not correlated with SAT. Now we have two sets of residuals from SAT, one for GPA and one for CLEP. GPA and CLEP are our two achievement measures. According to our theory, they should not be correlated except for the common influence of SAT. The residuals are what is left when we remove SAT from each variable. Therefore, our theory says that our two residuals should not be correlated.
If we compute the correlation between these two sets of residual, we find that:
|
CLEP resid |
GPA resid |
|
-.2053 |
-0.21266 |
|
-.36709 |
-0.13544 |
|
-.03797 |
0.01013 |
|
-.87342 |
0.03291 |
|
-2.53165 |
0.04177 |
|
1.30380 |
-0.08101 |
|
0.13924 |
-0.00380 |
|
5.63291 |
0.56456 |
|
-1.69620 |
0.01899 |
|
-1.36709 |
-0.23544 |
The correlation between the two sets is .73, which is significantly different from zero at p < .05. Thus we can reject our hypothesis that the correlation between GPA and CLEP is explained solely by SAT. Taking it a step further, we may seriously question the theory that the only common cause of the two achievement indices is math ability. Of course, there are always other explanations (our SAT is bad measure of ability? something strange about the sample? the courses that went into the computation of GPA, etc.).
The correlation between the two sets of residuals is called a partial correlation. In our case, it was the correlation between GPA and CLEP while holding SAT constant.
The partial correlation is what we get when we hold constant some third variable from two other variables. We know the correlation between CLEP and GPA is .88. But SAT "accounts for" (or could account for) part of that. What would happen to the correlation if SAT-Q were constant? It is .73, the correlation of the residuals from predicting CLEP and GPA from SATQ.
There are many substantive areas in psychology were we want to know partial correlations (Name 1?).
Pedhazur denotes the partial correlation r12.3 where r12 is the correlation between X1 and X2 and the .3 means the partial controlling for X3. In our example, it is the correlation between GPA and CLEP while holding SATQ constant.
The formula to compute the partial r from correlations is
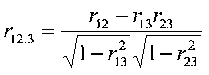
In our example, (1 = GPA, 2 = CLEP, 3 = SAT)
![]()
![]()
You won't be using this equation to figure partials very often, but it's important for two reasons: (1) the partial correlation can be (a little or a lot) larger or smaller then the simple correlation, depending on the signs and size of the correlations used, and (2) for its relation to the semipartial correlation.
If we partial one variable out of a correlation, that partial correlation is called a first order partial correlation. If we partial out 2 variables from that correlation (e.g., r12.34), we have a second order partial, and so forth. It is customary to refer to unpartialed (raw, as it were) correlations as zero order correlations. We can use formulas to compute second and higher order partials, or we can use multiple regression to compute residuals. For example, we could regress each of X1 and X2 on both X3 and X4 simultaneously and then compute the correlation between the residuals.
If we did that, we could be computing r12.34, the correlation between X1 and X2, controlling for both X3 and X4.
Partial Correlations from Multiple Correlations
We can compute partials from R2. For example
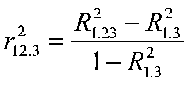
Of course we have some confusing terminology for you, but let's explore the meaning of this. This says that the squared first order partial (the partial of 1 and 2 holding 3 constant) is equal to the difference between two R2 terms divided by 1 minus an R2 term. The first R2 term is R21.23, which is the squared multiple correlation when X1 is the DV and X2 and X3 are the IVs (this is not a partial, it just looks that way to be confusing). The second R2 is R21.3, which is the squared correlation when X1 is the DV and X3 is the IV. This is also the term that appears in the denominator.
When we add IVs to a regression equation (first include them), R2 either stays the same or increases. If the new variable adds to the prediction of the DV, then R2 increases. If the new variable adds nothing, R2 stays the same.
|
|
B |
|
C |
|
In Figure A, the R2 for X1 will be the overlapping portion Y and X1 in the figure. When we add X2 to the equation, R2 will increase by the part of Y that overlaps with X2. Because X1 and X2 are orthogonal, R2 for the model with both X1 and X2 will be r2y1 + r2y2. In Figure B, when we put X1 into the regression equation, the R2 will be the overlapping portion with Y, that is, R2y.1 is UY: X1+Shared Y. When we add X2 to the equation, R2y.12 will be the total overlapping portion of Y with both X variables, that is, R2 will be UY: X1 + Shared Y + UY: X2. The increase in R2 that we see when we add X2 if X1 is already in the equation will be UY: X2.
Suppose we start over. We start with X2 in the regression equation. Then R2y.2 will be UY: X2 + Shared Y. If we then add X1 to the equation, R2 will increase to UY: X2 + Shared Y + UY: X1. In both cases the shared Y is counted only once and it shows up the first time any variable that shares it is included in the model. In Figure C, the variables overlap little, and the addition of each X variable into the equation increases R2. In Figure D, X3 overlaps completely with X1 and X2. If we add X3 after X1 and X2, R2 will not increase. However, adding variables never causes R2 to decrease (look at the figures).
Now back to the equation:
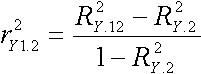
(I've changed symbols slightly to match the figures.) The term on the left is a squared correlation (a shared variance). On the right in the numerator is a difference between two R2 terms. It is actually an increment in R2. It shows the increase in R2 when we move from predicting Y from X2 (right term) to predicting Y from X1 and X2 (left term). Because R2 never decreases, R2y.12 will always be greater than or equal to R2y.2. The difference in R2 will be UY: X1, that is, the R2 due to X1 above and beyond that due to X2. The numerator is the shared variance of Y unique to X1 (UY: X1). So we have partialed out X2 from X1 on top. But we still have to remove the influence of X2 from Y, and this is done in the denominator, where we subtract R2Y.2 from 1.
The squared correlation is the percentage of shared variance (r2Y1.2). In figure B, the squared partial correlation of X1 with Y controlling for X2 will be UY: X1/[Total Y-(UY: X2+Shared Y)]. Note how X2 is removed both from X1 and from Y.
|
|
|
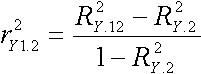
Semipartial Correlation
With partial correlation, we find the correlation between X and Y holding Z constant for both X and Y. Sometimes, however, we want to hold Z constant for just X or just Y. In that case, we compute a semipartial correlation. A partial correlation is computed between two residuals. A semipartial is computed between one residual and another raw or unresidualized variable. The notation r1(2.3) means the semipartial correlation between unmodified X1 and residualized X2, where X3 has been taken from X2.
Let's compare the correlational formulas for the partial and semipartial--
Partial:
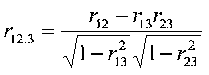
Semipartial

Note that the partial and semipartial correlation formulas are the same in the numerator and almost the same in the denominator. The partial contains something extra, that is, something missing from the semipartial correlation in the denominator. This means that the partial correlation is going to be larger in absolute value than the semipartial. This will be true except when the controlling or partialling variable is uncorrelated with the variable to be controlled or residualized; this is a trivial case.
Back to our educational debate. Suppose we want to predict college math grades. Someone argues that once we know CLEP (advanced achievement in math) scores, there is no need to know SATQ. SATQ will add nothing to the prediction of GPA once we know CLEP, says the argument. In this case we will want to partial CLEP from SAT, but not from GPA. That is, we hold CLEP constant for the SAT, and see whether the SAT so residualized can still predict GPA.
|
1. GPA |
2. SAT |
3. CLEP |
|
|
1. GPA |
1 |
||
|
2. SAT |
.72 |
1 |
|
|
3. CLEP |
.87 |
.88 |
1 |
In our example, (1 = GPA, 2 = SAT, 3 = CLEP)
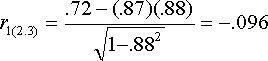
The correlation between GPA and SAT taking CLEP from SAT is -.096. This corresponds to the scenario of interest. It shows that there is basically no correlation between SAT and GPA when we hold CLEP constant. The other formula for the semipartial shows what happens if we partial CLEP from GPA but not SAT. This partial is shown below. It is not really of interest in the current case, but is presented anyway for completeness of computational examples.
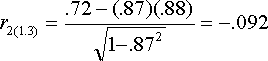
If we partial the CLEP from both GPA and SAT, the correlation is:
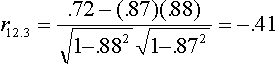
The result doesn't make much intuitive sense, but it does remind us that the absolute value of the partial is larger than the semipartial.
One interpretation of the semipartial is that it is the correlation between one variable and the residual of another, so that the influence of a third variable is only paritialed from one of two variables (hence, semipartial). Another interpretation is that the semipartial shows the increment in correlation of one variable above and beyond another. This is seen most easily with the R2 formulation.
Semipartial Correlations from Multiple Correlations
Let's compare partial and semipartial squared correlations:
Partial
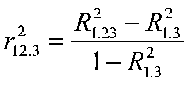
Semipartial
![]()
This says that the squared semipartial correlation is equal to the difference between two R2 values. The difference between the squared partial and semipartial correlations is solely in the denominator. Note that in both formulas, the two R2 values are incremental. That is, the left R2 is the squared correlation when X1 is the DV and X2 and X3 are IVs. The right R2 is the squared correlation when X1 is the DV and X3 is the IV. The difference between the two values, of course, is due to X2. The difference in R2 is the incremental R2 for variable X2. In terms of our Venn diagrams, X1 is Y, X2 is X1 and X3 is X2. Therefore, the squared semipartial correlation r2y(1.2) is R2y.12 - R2y.2 or UY: X1. The other semipartial would be R2y.12 - R2y.1.
Both the squared partial and squared semipartial correlations indicate the proportion of shared variance between two variables. The partial tends to be larger than the semipartial. To see why, consider our familiar diagram:
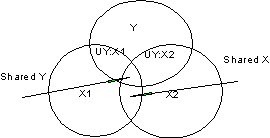
The partial correlation of X1 and Y controlling for X2 considers the ratio of UY: X1 to the part of Y that overlaps neither X variable, that is, UY: X1 to [Y-(Shared Y+UY: X2)]. This is because the partial removes X2 from both X1 and Y. The semipartial correlation between X1 and Y ry(1.2), however, corresponds the ratio of UY: X1to all of Y. This is because X2 is only taken from X1, not from Y.
In our example,
Y = GPA = variable 1
X1 = CLEP = variable 2; it's r with GPA was .8763, R-square is .7679.
X2 = SAT = variable 3; its r with GPA was .7181; R-square was .5156.
R-square for GPA on both SAT and CLEP was .7778.
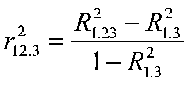

![]()
This agrees with our earlier estimate within rounding error, as .73*.73 = .53.
![]()
![]()
Earlier estimate:
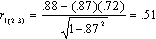
and .51*.51 = .26.
Regression and Semipartial Correlation
Regression is about semipartial correlations. For each X variable, we ask "What is the contribution of this X above and beyond the other X variables?" In essence, we regress each new X variable on the other X variables, and then correlate the residualized X with Y.
Note that we do NOT residualize Y each time we include an X.
That would be a partial correlation, not a semipartial correlation. The change in R2 that we get by including each new X variable in the regression equation is a squared semipartial correlation that corresponds to a b weight. The b weight provides a clue to answering the question "What is the correlation between {X residualized on the other X variables} and {Y}?" Another way of saying this is that the b weight tells us the slope of Y on this X while holding the other X variables in the regression equation constant.
Suppressor Variables
Suppressor variables are a little hard to understand. I have 3 reasons to discuss them: (1) they prove that inspection of a correlation matrix is not sufficient to tell the value of a variable in a regression equation, (2) sometimes they happen to you, and you have to know what is happening to avoid making a fool of yourself, and (3) they show why Venn diagrams are sometimes inadequate for depicting multiple regression.
The operation of a suppressor is easier to understand if you first think of measured variables as composites (simple or weighted sums) of other variables.
For example, we get a total test score that is the total of the scores on the items of a test. Or we get a job satisfaction overall score that is the total of the facet satisfaction scores. Now suppose that a composite is made by adding two things together that are negatively correlated with one another. For example, suppose we want to know your total attraction to an automobile and we get this by getting your satisfaction with cars by summing your satisfaction with attributes such as price and prestige. So we ask you to rate a bunch of cars on the attributes and we sum them. Now if you like the prestige, you won't like the price, and vice versa. If we add these two things, we get a total satisfaction score, but it has to parts to it that are antagonistic (negatively correlated) across cars. Note that this could happen even if we never asked you for ratings of multiple attributes, but rather asked for your overall satisfaction. Observed measures can be composites of lots of things, some positively correlated, some negatively correlated, and some uncorrelated.
Suppose we have two independent variables; X1 is correlated with the criterion, and X2 is not (or nearly so), but it is correlated with the first. Suppose we collected sales performance data (dollars sold per month) for a series of professional sales people (Y). Suppose we ask supervisors for judgment of sales performance for each, that is, how much they like their sales performance (X1). We also ask how much each supervisor likes each sales person as a person (X2). We have collected some data on these three variables and find that the results can be summarized in the following correlation matrix:
|
|
Y |
X1 |
X2 |
|
Y |
1 |
|
|
|
X1 |
.50 |
1 |
|
|
X2 |
.00 |
.50 |
1 |
Note that X1 is correlated with Y. X2 is not correlated with Y, but it is correlated with X1. In this case, X2 will be a suppressor. We can solve for beta weights by R-1r = b.
|
R = |
1 |
.50 |
|
r = |
.50 |
|
|
|
|
.50 |
1 |
|
|
.00 |
|
|
|
|
|
|
|
|
|
|
|
|
R-1 = |
1.333 |
-.667 |
|
b = |
.667 |
(b1) |
|
|
|
-.667 |
1.333 |
|
|
-.333 |
(b2) |
|
Note that the beta weight for X2 is negative although the correlation between X2 and Y is zero. This can also happen sometimes when r for X2 is (usually slightly) positive.
Note also that the beta weight for X1 is positive, and actually larger than its corresponding r of .50. The R2 for the two variable model is (.50)*(.667) or .334. This is larger than .502 or .25 that would have been guessed solely on the basis of X1 (X2 might have been disregarded because of its zero correlation with Y). How can this happen? Three ways to explain the suppressor variable.
Let's return to the three reasons for learning about suppressors. First, inspection of the correlation matrix may be insufficient to tell the value of a variable in a regression equation. It turns out that X2 was a valuable contributor to predicting Y, and this would not have been obvious from simply looking at the correlations of each X with Y. With just two IVs, you can tell that suppression is likely because of the pattern of correlations. With larger numbers of variables, it becomes increasingly difficult to see what will happen in regression just by looking at R.
Looking like a fool. Always look at your correlations between each X and Y. If the signs of r and b are opposite, you most likely have a suppressor. Do not interpret the negative b weight as if the r were negative. It may be better to interpret the variable with the positive r and negative b as a measure of error of prediction in the set of IVs. You should at least point out to your reader that b and r have opposite signs.
The problem with Venn diagrams. The difficulty here is that in the initial setup, X2 and Y are not correlated, so the circles do not overlap. After partialing X1 from X2, however, X2 and Y are negatively correlated, so the circles do overlap. It's hard to draw 1 circle that both does and does not overlap another circle.