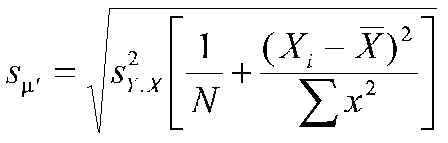
Prediction
Objectives
Why is the confidence interval for an individual point larger than for the regression line?
What is cross-validation? Why is it important?
Why does shrinkage in R-square occur?
Describe the steps in forward (backward, stepwise, blockwise, all possible regressions) predictor selection.
What are the main problems as far as R-square and prediction are concerned with forward (backward, stepwise, blockwise, all possible regressions) predictor selection?
Why is predictor selection to be avoided when explanation is an important part of the research question?
Materials
The subtitle to Pedhazur's book is "Explanation and Prediction." One of the main uses of regression is to predict a criterion from one or more predictors. We might want to predict who will succeed in training (e.g., graduate training in psychology, flight training, medical school), who will repay a loan or get into an accident, who will perform well on a job, who will get along with other people in tight quarters over long periods of time (submarines, arctic expeditions, or space flight). In some applied contexts, our only interest is in predicting what will happen, not WHY it happens. As soon as we begin to talk about why something happens, we are talking about explanation.
In selecting pilots who would complete the flight training successfully, psychologists used everything they could think of. One of the questions they developed was something like this: "As a child, did you ever build model airplanes that flew?" It turns out that this one question was about as effective in predicting pilot training success as the rest of the entire psychological battery. It may seem obvious to you why this item was useful (interest in flight). However, two other useful items were "Does being in high places make you nervous?" and "What is your favorite flavor of ice cream?" The high places item was odd because answering that high places make you nervous was indicative of success in pilot training. I don't know what the good and bad flavors of ice cream were - the point is that responses to the item were useful to the armed forces for making decisions no matter what the reason. In applied contexts, prediction can be very useful even if we don't know why it works.
In an academic context, however, we always want to know why things work the way they do -- this is what theory is about. A measure that is highly correlated with another measure may add very little to a prediction equation, but it may be crucial for theoretical reasons. In a group of normal adults, all cognitive ability measures tend to be highly correlated. Adding a test of say, analogies, may add little to prediction if we already have tests of verbal comprehension such as synonyms, antonyms, or paragraph comprehension. However, the verbal reasoning involved in the analogies test might be crucial for the explanation of the dependent variable.
Confidence Intervals for Predicted Scores
Standard error for the mean of predicted scores at a given X is:
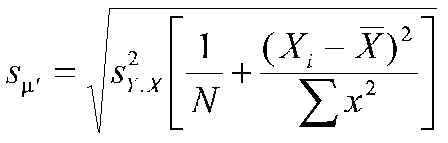
where s2Y.X is the variance of estimate, or mean square residual, N is the sample size, Xi the score of these people on the predictor.
Confidence Interval of the mean of predicted score, that is, the confidence interval for the regression line:
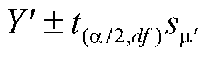 :
:
Standard error for the predicted score (single predictor)
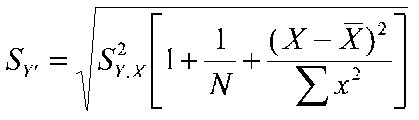
Confidence Interval for individual scores:
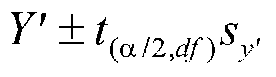
The standard error for the mean is smaller. A graph of both using data from the last lecture:
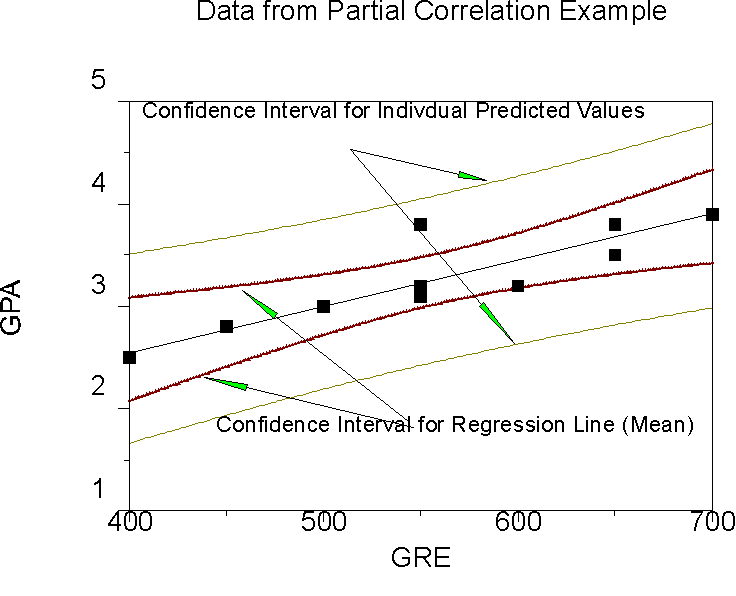
In both cases, the confidence interval is larger as we move away from the means of X and Y. This is to account for the sampling distribution of the regression line. The confidence band for the line itself is that for the mean of Y given X. The confidence band for the mean is smaller than for the individual because there is less error in estimating the mean of scores than in estimating an individual score. The difference is in estimating how people in general who score 500 on the SAT or GRE will do versus estimating how this individual person will do. With individual people, we have to consider the whole distribution of Y at that given X. With the regression line, we have to consider a sampling distribution of MEANS of Y at that given X.
Shrinkage
When we estimate regression coefficients from a sample, we get an R2 that indicates the proportion of variance in Y accounted for by our predictors. This R2 is biased. It is generally too large because we capitalize on chance fluctuations in the correlations to maximize R2 (minimize the sum of squared errors; the estimation technique is least squares). We need to shrink R2 to be correct. When R2 is zero in the population, the expectation in the sample (expected value or mean of the sampling distribution) is:
R2 = k/(N-1)
where k is the number of predictors and N is the sample size. If we have two people and 1 predictor, we have an R2 of 1. With 2 people, there is a straight line that connects them and there is no error of prediction because both people fall right on the line. Whenever there are lots of variables and not so many people, we can get very large R2 values just by using lots of variables (R2 approaches 1 as the number of predictors approaches the number of people). Early researchers failed to realize this and reported huge R2 values with small numbers of people and large numbers of variables. You could predict things using survey items as variables and achieve any desired R2. Or in selection, you can use test items as variables to get any desired correlation. Of course, this is unethical and should be avoided. We can adjust our sample R2 to reduce the bias. The most commonly used formula is:
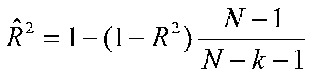
Where ![]() is the adjusted or shrunken estimate. This estimate accounts for differences in the size of the original R2, the sample size, and the number of predictors. This formula is used by SAS and reported as an adjusted R2. All the shrinkage formulas say that shrinkage will be more of a problem when the sample R2 is small, N is small, and k is large.
is the adjusted or shrunken estimate. This estimate accounts for differences in the size of the original R2, the sample size, and the number of predictors. This formula is used by SAS and reported as an adjusted R2. All the shrinkage formulas say that shrinkage will be more of a problem when the sample R2 is small, N is small, and k is large.
Suppose R2 is .6405 with 4 predictors and a sample size of 30. Then
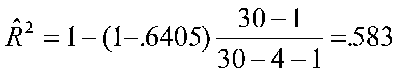
If the sample size were 100 instead of 30, ![]() would be .625; if N were 15, then
would be .625; if N were 15, then ![]() would be .497.
would be .497.
Supposing the sample R2 was .30, then the adjusted R2 would be
![]() = .020 for N = 15
= .020 for N = 15
![]() = .188 for N = 30
= .188 for N = 30
![]() = .271 for N = 100
= .271 for N = 100
Cross-Validation
Suppose we compute regression estimates on a sample of people. We then collect data on a second sample, but we do NOT compute new values of a and b for this sample. Instead, we compute predicted Y values using the coefficients from the previous sample. We then find the correlation between Y and Y' and square it. This gives us a cross-validated R2. Because we have not estimated b weights, there will be no capitalization on chance, and our estimate of R2 should be good on average. It tells us what the correlation to expect when we actually use the equation.
Double Cross -Validation
If we collect a second sample to use for cross validation, we can use them as another derivation sample, too. We get two samples. For each sample we compute regression estimates and compute an R2 on that same sample. This gives us two biased R2 estimates. Now we cross validate each set of weights on the other sample, and we have two cross-validation R2 values. The average of these is our best estimate of cross-validated R2. If we want the best estimates of our regression coefficients, we can combine our samples.
Data Splitting
Collecting new samples for cross validation isn't a great idea. It costs time and money. If the samples are different and the regression results differ with the samples, you have a whole new problem. It is usually preferable to collect data on a large number of people (say 500) and split the data randomly into two equal sized pieces for cross validation.
I have seen a sort of cross validation once where there was no estimation of weights. An industrial psychologist familiar with certain tests picked (made up) the weights and applied them to the test battery. Thus there was no capitalization on chance and no shrinkage. Don't do this unless you have lots of experience. Humans are not too good at guessing regression weights.
We can estimate cross validation results using formulas. Pedhazur describes two such formulas, one in which the predictors are fixed, and one in which they are random. For the fixed case:
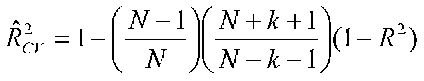
For the random case:
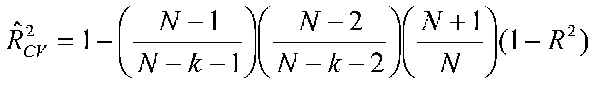
If we have 30 people an R2 of .6405 and 4 predictors, then for the fixed case, we have:
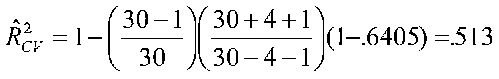
For the same data for the random case, we have:
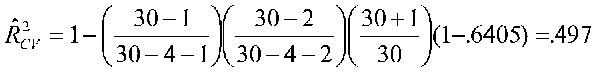
For the same data, our adjusted R2 (adjusted for shrinkage, not cross-validated) was .58.
My grasp of the real meaning of fixed and random cases in the analysis of data has never been the best. Let's say for the sake of discussion is that we get the fixed case when we select the values of X deliberately to represent something. For example sex (0,1) and study time (5 min to 2 hours in 5 min blocks) are fixed. The random case obtains when the X values are sampled, as would be the case of we measured people on IVs such as age or SAT scores.
It is always the case that we cannot legitimately apply regression results beyond the data for which they were obtained. For example, if we compute a regression equation where the maximum X is 10 and the minimum X is 0, then we have no business interpreting Y' values for X greater than 10 and X less than 0. This is generally not a problem for the fixed case, where we include all values of X that are of interest. It can be a problem for the random case, where the values of X can vary across studies.
Predictor Selection
In applied contexts, you may wish to select a set of predictors from a larger set so as to maintain most of the R2 from the larger set, but gain economy by having fewer predictors. It is especially desirable to eliminate expensive predictors. Although I am going to show you how to do this, most of you will never have an opportunity to use these techniques properly. You will have many opportunities to misuse them, however, and I urge you to avoid using any of these unless you are convinced that you are interested ONLY in economy of prediction, that is, maximizing R2 while minimizing cost. NEVER use these if you are interested in explaining variance in the dependent variable. When you want to explain things, use simultaneous regression (include all variables of theoretical interest). You may also use hierarchical regression, in which you specify a series of regression equations based on theory so that the equations are specified before the data are collected. When you want to explain things, you may wish to use one of the techniques more advanced than multiple regression, such as path analysis or structural equation modeling. At any rate, you won't be using predictor selection algorithms.
The techniques we will discuss for selecting a subset of predictors are called (a) all possible regressions, (b) forward selection, (c) backward selection, (d) stepwise, and (e) blockwise.
All possible regressions
With this approach, you start with each 1 variable model and compute an R2 (of course, this is the squared zero order correlation). Then you compute R2 for each pair of predictors. Then you compute R2 for each triplet of predictors, and so forth until you have 1 model with all k predictors in it. Now you can clearly see the R2 for every model. You can choose the model with the largest R2 for any number of predictors. If you have 4 variables, you could choose the model with all 4, or the model with 3 predictors with the largest R2, or the model with 2 predictors with the largest R2, and so forth. This is a good method if you want to be certain to maximize R2. With no other method can you be sure you have the maximum R2 for the given number of variables (except for all k and with the first 1). The drawback is that with a large number of predictors, there will be a (very) large number of models. For example, with 12 predictors, there will be 212 or 4096 regression equations and therefore R2 values.
Example from Pedhazur
|
|
GPA |
GREQ |
GREV |
MAT |
AR |
|
GPA (Y) |
1 |
|
|
|
|
|
GREQ |
.611 |
1 |
|
|
|
|
GREV |
.581 |
.468 |
1 |
|
|
|
MAT |
.604 |
.267 |
.426 |
1 |
|
|
AR |
.621 |
.508 |
.405 |
.525 |
1 |
|
Mean |
3.313 |
565.333 |
575.333 |
67.00 |
3.567 |
|
S.D. |
.600 |
48.618 |
83.03 |
9.248 |
.838 |
All possible regressions for these data looks like this:
|
Number in Model |
R-square |
Variables in Model |
|
1 |
.385 |
AR |
|
1 |
.384 |
GREQ |
|
1 |
.365 |
MAT |
|
1 |
.338 |
GREV |
|
|
|
|
|
2 |
.583 |
GREQ MAT |
|
2 |
.515 |
GREV AR |
|
2 |
.503 |
GREQ AR |
|
2 |
.493 |
GREV MAT |
|
2 |
.492 |
MAT AR |
|
2 |
.485 |
GREQ GREV |
|
|
|
|
|
3 |
.617 |
GREQ GREV MAT |
|
3 |
.610 |
GREQ MAT AR |
|
3 |
.572 |
GREV MAT AR |
|
3 |
.572 |
GREQ GREV AR |
|
|
|
|
|
4 |
.640 |
GREQ GREV MAT AR |
Note how easy it is to choose the highest R2 model for any given number of predictors. You have to factor in how much loss in R2 is tolerable and what the various tests cost to make a determination of which one to choose.
Forward
For forward selection you (the computer) start with a simple model and build up. The first variable to enter the equation is the variable with the largest zero order correlation (this gets the largest single variable R2). Then compute the squared semipartial correlation between Y and the rest of the X variables (this is the same as: figure the increment in R2 for each new variable when the first is already in). Choose for the second variable that which has the largest increment in R2 given that the first is already in. Now we have two variables in. For the third variable, find the increment in R2 for each of the remaining variables given that the first two are already in. Choose the variable that has the largest increment in R-square to be the third, and so on. When to stop? We usually tell the computer that we want to keep going so long as there is a substantial increase in R2. When there is no reasonable increase in R2, we stop, whether there are no variables included or all of the variables in the original set are included. A common way to tell the computer what is reasonable is to use a function of F. For example, we can choose a probability of F of less that .05 as an entry criterion. (PIN=.05 or probability of F to enter is less than .05).
A major drawback to forward selection is that once a variable is in, it stays, even if it is no longer useful. For example, AR will be picked first in our example because it has the highest zero order correlation with GPA. It will never be removed, even though it is useless in the predictive sense after some other variables are included in the regression equation.
Avoid forward selection; it is described here to help you see how another technique works.
Backward
Backward selections is sort of the inverse of forward selection. With backward selection, we start with all variables in the equation, and then we dump them one at a time if they do not command a reasonable increment in R2 beyond the other variables in the equation. If at the first step, all of the variables are associated with a substantial (meaningful, significant, etc.) incremental R2, the process terminates without reduction in the number of predictors. If one is eliminated, then the regression is recomputed and we examine all the remaining variables to see if one has a minimal incremental R2. If yes, we dump it and try again. The process terminates when we examine an equation and decide that all the variables have a substantial incremental R2. Here we can run into the opposite problem of that encountered in forward: a variable eliminated early on could be valuable later, but overlooked.
Stepwise
Stepwise combines both forward and backward selection strategies. It starts by choosing as the first predictor that variable associated with the largest zero order correlation. At the second step, just as in forward, it computes the increment in R2 for the rest of the predictors and includes that variable with the largest incremental R2 as the next predictor. At this point, however, it goes back and checks the incremental R2 of the first variable to see if it is still useful after entering the second variable. If both variables are still useful, we go to choosing the third variable just as in forward selection. If the first variable is no longer useful, it is pulled out of the equation and set aside. We now have a new first variable, and we will compute an increment in R2 for the rest of the other variables over this new one. We will choose for entry that which is the largest. At each step, we will make a choice for entry and also check for variables in the equation that are no longer useful. We stop when neither adding nor subtracting variables results in an improved regression equation. This algorithm is intended to provide an efficient means of reducing the set of predictors. It works better than either forward or backward selection alone. Unlike all possible regressions, it does not guarantee resulting in the highest possible R2 for a given number of predictors. It is very popular for reasons that appear to have little to do with its effectiveness.
Blockwise
With this approach, forward selection is applied to sets of variables (blocks). Any of the methods (e.g., stepwise) are used within blocks to select the variables to represent each block. Each block consists of two or more measures of a construct, such as measures of socioeconomic status; another block might be composed of measures of verbal ability. For step 1, the representative SES measures are chosen using a stepwise algorithm. The survivors are entered as a block, and frozen there (forward selection). The next block, verbal ability measures, is then considered. They are chosen through a stepwise analysis with the SES indicators forced to stay. Then the verbal ability survivors are entered as a block, and stay in the equation while we examine the next set of predictors. We stop when the latest block isn't adding anything.
Blockwise is useful in applications where the sets of variables differ in cost or ease of collection.
We may start with demographic data that come from the application blank (or from a profile taken from the internet). Then we add paper-and-pencil tests, which are relatively cheap. Then we add tests (such as an in-basket) that are individually administered by a psychologist. Imagine sets of data in school systems (demographics, past grades, standardized test scores, teacher ratings, school psychologist evaluations, etc.) used to predict deviancy or dropout.
Things to consider about predictor selection
Variables chosen by predictor selection to remain in the equation may be virtually indistinguishable from others chosen for exclusion from the equation. The sole difference may be chance fluctuation in r that resulted in one or the other being chosen. Therefore, do not interpret the survivor status as meritorious in any substantive sense other that pure predictive effectiveness in the current context.