What is a latent variable? What is an observed (manifest) variable? How does SEM handle measurement errors? Why does SEM have an advantage over regression and path analysis when it comes to multiple indicators? What are the two submodels in a structural equation model? What are their functions? How are observed correlations linked to the parameters of a structural equation model (via the diagram, that is)? Why can't we conclude cause and effect from structural equation models where there is no manipulation of variables? What is the danger of model fiddling?

Path analysis is a special case of SEM. Path analysis contains only observed variables, and has a more restrictive set of assumptions than SEM. Most of the models that you will see in the literature are SEM rather than path analyses. The main difference between the two types of models is that path analysis assumes that all variables are measured without error. SEM uses latent variables to account for measurement error.

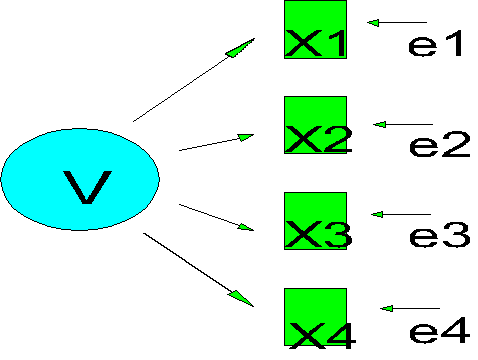
A latent variable is a hypothetical construct that is invoked to explain observed covariation in behavior. Examples in psychology include intelligence (a.k.a. cognitive ability), Type A personality, and depression. In the psychometrics literature, latent variables are also called factors, and have a rich history of statistical developments in the literature on factor analysis. The basic idea is that a latent variable or factor is an underlying cause of multiple observed behaviors. For example, suppose we have a test of vocabulary. The variance in response to each item in the test reflects individual differences in verbal ability across test takers, plus some error. In factor analysis, we would represent such a test as

Where V stands for the latent variable vocabulary, X1 through X4 stand for the items in the test, and e1 through e4 stand for measurement errors (unreliability) in each item. [Technical digression - the errors in factor analysis are actually measurement error plus stray causes, but the implications are the same for our purposes.] Points to notice:

1. We are assuming a single latent variable (factor) that corresponds to vocabulary.
2. The factor is assumed to cause the observed correlation among the 4 items.
3. The correlation among the items would be 1.0 except for the errors. [Recall the beginning of the course when we talked about what happens to correlations when we add random error to the observations.]

It turns out that the expected correlation between two variables that share a single factor is equal to the product of the two paths from that factor (analogous to a spurious effect in path analysis).

For example, suppose the path from V to X1 is .8 and the path from V to X2 is .9. Then the expected correlation between X1 and X2 is .72 (.72 = .8*.9). Recall that the correlation between X1 and X2 would be 1.0 if there were no measurement error. Therefore, measurement error accounts for the difference between the correlation of .72 and 1.0. That is, the correlation is reduced toward zero by the inclusion of less than perfectly reliable measures. Observed variables typically have some measurement error associated with them, and so their correlations with other variables are attenuated (too close to zero) due to the presence of this measurement error. Latent variables, on the other hand, are not directly measured and do not have measurement error associated with them. This is kind of a big deal because if we can estimate the association of latent variables, we can estimate the relations among variables without measurement error.

[Technical digression. There are ways to account for unreliability of measures for both correlation and regression coefficients, and to do so without estimating paths to assumed latent variables. That is, we can estimate the effects of unreliability directly with our observed variables. Both positions (with and without latent variables) have some merit.]

The other advantage of latent variables is that multiple indicators of the same construct are naturally handled with a structural equation model. In a regression model, multiple indicators cause collinearity problems and small increments in variance accounted for.

Most people follow the notation used the computer program LISREL (LInear Structural RELations) to talk about structural equation models. We can use the following diagram to illustrate the main points:

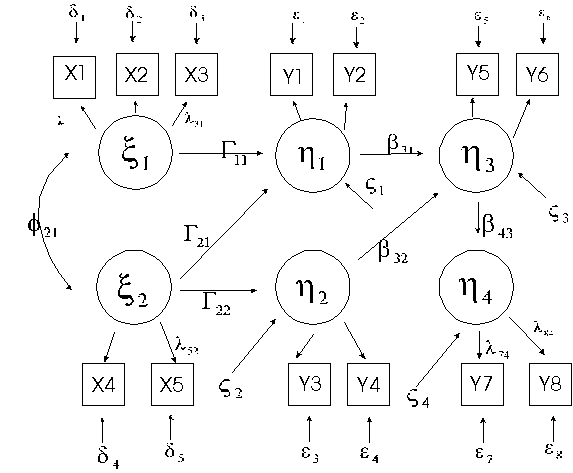
The latent variables or factors are indicated by circles. The observed variables are indicated by squares. The observed exogenous variables are labeled X. The latent exogenous variables are labeled ksi (x ). The observed endogenous variables are labeled Y; the latent endogenous variables are labeled eta (h ). The paths from the latent to the observed variables are labeled lamda (l ). The paths from the exogenous to the endogenous variables are labeled gamma (G ). The paths from the endogenous variables to other endogenous variables are labeled beta (b ). The correlations among the exogenous variables are labeled phi (f ). Finally, there are three kinds of errors. One kind of error is a stray cause of the latent endogenous variables, called psi (z ). There are also errors of the observed variables. For the observed exogenous variables, these errors are called delta (d ) and for the observed endogenous variables, these errors are called epsilon (e ). Each of these is labeled in the figure. (Not all labels for paths from the latent to the observed variables are included in the figure.)

Just as in path analysis, the diagram for the SEM shows the assumed casual relations. If the parameters of the model are identified, a covariance matrix or a correlation matrix can be used to estimate the parameters of the model, one parameter corresponding to each arrow in the diagram.

I am going to make up numbers for structural (path) coefficients for the model. Then I will present them in matrices that correspond to their LISREL notation. Finally I will combine them according the set of equations implied by the model to generate a correlation matrix. The path diagram looks like this:

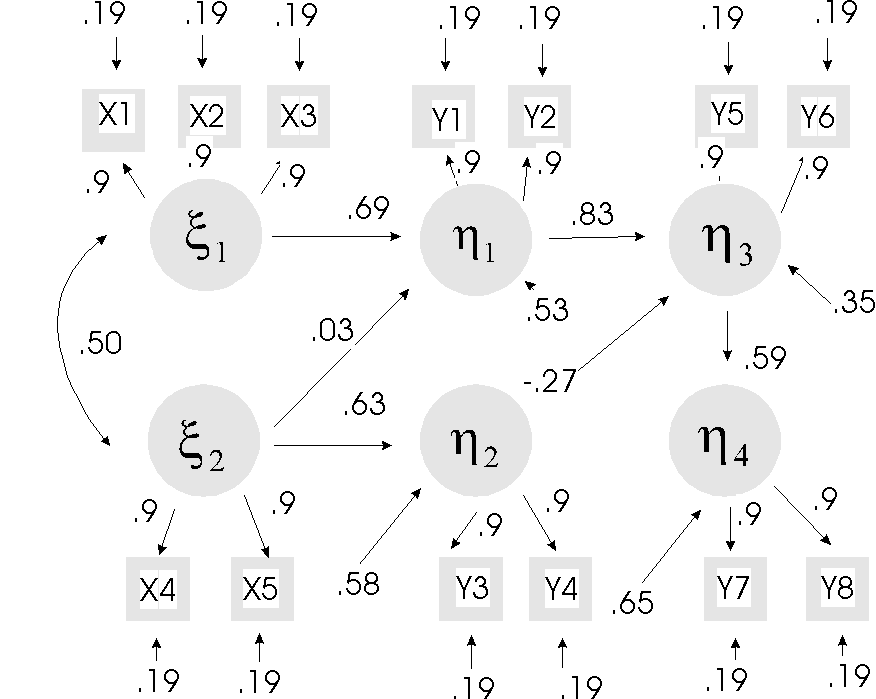
There are two parts to a structural equation model, the structural model and the measurement model.

For the structural model, the equations look like this in matrix form:

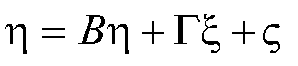
This is an equation for predicting the values of endogenous variables (DVs). It says that the DVs are a function of the endogenous effects on themselves (the beta-eta part) plus the effects of the exogenous variables on the endogenous variables (gamma times ksi) plus the stray causes.

In our example, we have:

If we substitute the numbers from the diagram, it looks like this:

Notice that beta (b ) and gamma (G ) are sets of parameters (path coefficients). The other entries --eta (h ), ksi (x ) and psi (z )-- are latent variables. This is the structural part of the model. It indicates how the latent variables are related.

The other part of the model is the measurement model. The measurement model indicates how the latent variables related to the observed variables. In our example, there are two parts, one for the exogenous variables and one for the endogenous variables:

Our parameters were:

Notice that we have the path coefficients (L _X) leading from the latent exogenous variables to the observed variables. These are the parameters of the model. The other items are variables.

For the endogenous variables, we have:

Our parameters were:

Here again we are looking at the paths that relate the latent endogenous variables to the observed endogenous variables.

To link the parameters of the model to the observed correlation matrix, note first that the correlation matrix can be split into 4 pieces:

To find the observed correlations in each of the four part of the correlation matrix, we need a different expression (well, the upper right and lower left are really the same). In one section we only have X variables, in one we only have Y variables, and in the other two, we need an expression for both X and Y. It turns out that the expressions for the correlations are:

These equations may look a bit ugly (the sort of equation that only a mother could love), but remember that all we have here are a few matrices to add, subtract, multiply or invert. All of these except the error terms (theta & psi) are paths. Let's look at a couple of examples.

First, let's look at the correlations of the 5 observed X variables.

X with X

Note: the column for theta (q d ) is actually a diagonal matrix, that looks like this:

With a matrix of this order, we can add it to the product of the prior three matrices. It wouldn't fit on the same page in the table in its diagonal form, so I showed it as a column. The result of multiplying and adding the above matrices is the correlation matrix of the observed X variables:

The correlations among the observed variables that belong to the same latent variable are all .81, because the paths from the latent variables to the observed variables are all .9, and we multiply the paths to get the expected correlation (.9*.9 = .81). The expected correlations among the observed variables with different latent variables are each equal to the path from the observed variable to the latent variable times the correlation of latent variables times the path from the latent variable to the other observed variable, that is .9*.5*.9 = .81*.5 = .405. Look at the path diagram to see how this works in the model.

One of the combinations of X and Y is

The first part of the equation:

 The second part of the equation

Total result: 8 x 5 (Y by X)

If we carry out the matrix operations, we get:

Remember that there are three observed X variables (X1 to X3) for the first latent X, and the other two X variables refer to the second latent X. The Y variables come is pairs, one pair for each latent Y. To find the correlation between each X and each Y, we trace from one to the other, multiplying coefficients on a tracing and adding across tracings. (See the path diagram.) For example, suppose we want to know the correlation between X1 and Y1. There are two ways to get there - one direct path and one through the correlated cause.

For the direct path, we have .9*.69*.9 = .5589. For the indirect path, we have .9*.50*.03*.9 = .01215. When we add them together, we have .57105. Within rounding error, this is .57, which is what is shown in the table. The point of this exercise is to show you that SEM, just like path analysis, has a path diagram that implies a set of equations. The equations imply a set of correlations that can be tested against data that you collect. On the other hand, you can collect data (correlations) that will allow you to estimate the parameters contained in the equations.

Can you draw causal conclusions from an ordinary regression equation if the data were not collected from a design where the independent variable was manipulated?

(No, no, nooo, no.)

Path analysis is just a series of regressions applied sequentially to data. Can you draw causal conclusions from path analysis where no variables were manipulated? [It's just regression...]

SEM is basically just path analysis with latent variables. Can you draw causal inferences without manipulation in SEM? Incidentally, strictly speaking, manipulation doesn't allow one to draw causal inferences. It just helps to rule out LOTS of alternative explanations. In SEM we can fit the data with parameters, but we rarely to never rule out alternative explanations.

If you work in an area in which nonexperimental designs are common (industrial / organizational psychology and clinical psychology to name two), you must study SEM because it is widely used and is becoming required by reviewers for data analysis. Never mind that the reviewers are pretty much clueless about how to do this properly or even what it means. You still have to do it. All I have been able to do is introduce you to SEM concepts at an elementary level. You should take a course in it.

The big advantage of SEM. SEM allows for tests of theoretical propositions in nonexperimental data. You can test whether the factor structure of job satisfaction or the relations among personality characteristics is the same in the U.S. versus Japan with this. You can test whether a reciprocal path accounts for a specific relation in your data better than does a one-way causal flow. You can test quantitative predictions (e.g., the theory says that the path is .80) against data. This is powerful stuff.

What most people don't recognize. The power of the technique is rarely realized. It is very strong when you have parameters in mind and you want to test them against the data. People generally do not have any parameters in mind; they estimate them instead. To identify the problem (that is, to solve the identification problem so that all parameters have unique values), researchers assume that some parameters are zero in the population. The test of the model becomes a test of whether those parameters are zero in the population. This is generally not true (they are not zero in the population) and generally not very interesting (we are really interested in the parameters we estimated but did not test). That's not why this stuff was developed, but that's how everyone uses it. So far as I can tell, the situation is unlikely to change.

Model Fiddling. People develop a model, collect data, estimate the parameters, look at the fit statistics to see how well their data fit the model, and discover that the data fit the model rather poorly. This is roughly analogous to spending a year doing an experiment and having nonsignificant results. When this happens, it is definitely not okay. What do you do? Well, people begin fiddling with the model to make it fit. This usually takes a minimum of 1 month, and the resulting good-fitting model is generally not something you would have specified in advance. For this reason, I try to avoid doing SEM when I can. In my opinion, we generally don't have enough information to use the technique properly, that is, to conduct specific tests of meaningful hypotheses. However, my views on SEM are less enthusiastic than those of most researchers, who feel that its advantages outweigh its problems.