Why does the order of entry in a prediction equation change the incremental variance accounted for by a variable?

What is commonality analysis? How is it used?

How can a variable be important from an understanding point of view even if its unique proportion of variance is small?

When IVs are uncorrelated, a simple index of the importance of the variables is the zero order correlations of each IV with the DV. When IVs are correlated, things are not so simple. There is no way to assign variance in Y that is shared by more than one IV to a particular IV. Well, there are actually lots of ways to make that assignment, but they are all problematic. To see the problem, suppose we have three variables that look like this:

Is the change (variance) in Y due to X1 or to X2? There is no way to tell from the information given. There is no instance when X1 goes one way and X2 goes another, so we cannot disentangle their effects. People sometimes infer the importance of the X variables by looking at the variance in Y accounted for by each X. This is typically done by finding increments of variance accounted for. This is sometimes called hierarchical regression because we order the entry of variables into an equation and check for R² change at each step.

Let's recall the example from last week:

The unique variance attributable to each variable (GREQ, GREV, MAT, & AR) is equal to the difference in R² between the model with all 4 IVs and the model with that particular IV missing. The R² for the full model (all four IVs) is .640. The difference between that model and each of the 3 variable models shows the unique contribution of each:

The numbers in the right most column are the proportion of variance in Y uniquely attributed to each X. These numbers correspond to SAS Type III sums of squares (in PROC GLM) for the simultaneous regression with all 4 variables included. If we take the sum of squares for the entire model (total sum of squares) and divide the Type III sums of squares for each variable by the total, we will get the proportions shown in the table above.

The test of b weights in a simultaneous regression (all variables included) is equivalent to testing the unique proportion of variance for that variable, and this is equivalent to testing the increment in R² when that variable is added to the equation last. So if we put all 4 variables into a regression equation, the Type III sum of squares for each divided by the total would give the numbers in the right hand column of the table. These numbers can also be obtained by subtracting R², as we did in the table. The significance of the incremental R² values is identical to the significance of the b weights in the simultaneous regression.

When the IVs are uncorrelated, R² is the sum of the zero order correlations. This is no longer true when the IVs are correlated. Instead, R² is composed of several different pieces. When the IVs are correlated, R² can be decomposed in several different ways, and these are not equivalent. The sequence of control or steps used to add variables to the equation matters. For example, let's start with AR.

Some points to notice: the total R² for the four variables is .640. If we add the right-most numbers, we get .385+.118+.107+.030 = .640, the total R². However, only the last difference (.030) agrees with our uniqueness index. The sum of the unique parts is .023+.030+.068+.068 = .189, less than 1/3 of the R² of .640. The attribution of R² to the variables in order favors the variables first entered because they get the shared part attributed to them. Let's do the analysis once more, but change the order of entry.

Points to notice: The contribution of each variable is different in this analysis. The only item that agrees with our original analysis is .023 for AR, and this is because AR is the last variable in the equation. Incremental R² is only constant when the IV is the last in; otherwise the order matters. What do you say when someone shows you a table like this where there is a series of variables entered, a change in R-square in each step, and then they go on to talk about the importance of each variable based on the change in R-square in each step? (The short answer is b.s. You have to see the entire correlation matrix. If the IVs are all orthogonal, then a table like those two above is fine. Otherwise, the contribution for each depends upon where it is entered and will most likely be misleading.)

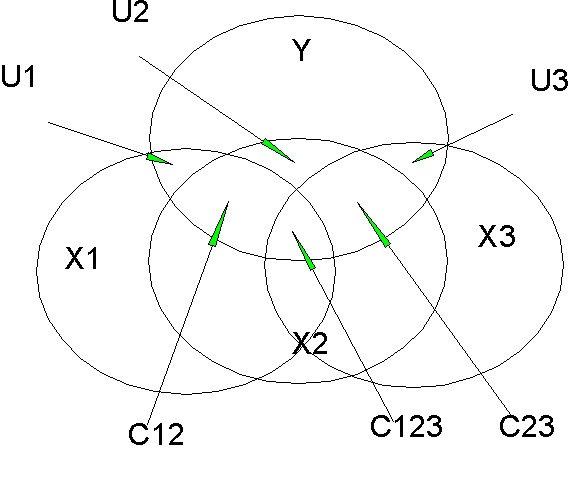
Here we have 1 DV (Y) and 3 IVs (X1-X3). All have substantial intercorrelations. We can assign variance in Y to X1-X3 according to their unique contributions (U1, U2, & U3) and their various shared parts (C12 is the shared part for X1 and X2; it doesn't count U1 or C123).

We can find any of these areas with a little work. For example, C23 is

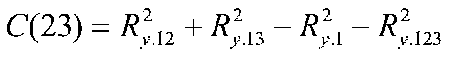
This formula isn't very obvious, but with a little addition and subtraction we can find every part of the diagram. The neat thing is: now we can divvy up the shared part so we can assign variance in Y to the unique parts of the three Xs, their shared pairs, and the triplet. We can do this for larger numbers of IVs, but it gets out of hand pretty quickly. Such an analysis is informative for prediction purposes. It tells us where the variance in Y is coming from.

Folks are tempted to equate variance accounted for with importance of variables. This is fine in a predictive case, but not in an explanatory case. If you are interested in explanation and you do this, it means that you haven't thought out your theoretical position fully. The importance of variables can only be examined properly from a specific theoretical view. The calculations flow from a theoretical position. For example, suppose you think that SES explains the correlation between SAT and GPA in a college. You reason that the SAT is written by and for rich people, and that the college environment is more or less social preparation for the rich, so the correlation between SAT and GPA is spurious, that is, the observed relations between SAT and GPA are not due to aptitude predicting achievement, but rather to something else entirely. We could diagram our thinking like this:

In diagram A, it would make sense to compute a partial correlation to find the relations between SAT and GPA while holding SES constant (this is consistent with our theoretical scenario). This is not the same as an incremental R². In diagram B, we have a different assumption about the causal relations among these three variables. This is a different theory. It says that SES causes differences in SAT. SAT in turn causes differences in GPA. It also says that SES has a direct effect on GPA. In this case, we can think of the variance in GPA as due to a direct effect of SAT on GPA, a direct effect of SES on GPA, and an indirect effect of SES on GPA through SAT.

There are methods used to compute direct and indirect effects that we will cover in path analysis. For now it is enough to know that they do not correspond to the uniqueness (difference in R²).

Path analysis will allow things to be both highly correlated and show large effects. Based on diagram B, for example, SES could have a large indirect effect if all three variables were highly correlated (SES influences SAT which influences GPA). Such a result would indicate that SES was important though its influence on SAT. This is a rather different conclusion than might be reached looking at the unique contribution of SES in predicting GPA.

Here I offer some general advice on choosing the model to analyze your data. Unless you have no interest in explanation, avoid the variable selection algorithms. If you just want to achieve efficient prediction, don't use stepwise, use all possible regressions instead.

1. No matter how many IVs you have, always present a correlation matrix of the DV and all IVs. Include means and standard deviations for the variables as part of this matrix.

2. If you have only 2 IVs, compute the simultaneous regression with both IVs. Unless you have interactions, curves, or some other funky term that requires an extra IV, you're done. The unique R-square for each can be found by comparing the squared zero order correlations to the R-square for the model with both IVs in it. The significance of each b weight tells whether the increment in R-square is significant for that variable.

3. If you have interactions or curves, you will want to use hierarchical regression. Refer to the section on curvilinear regression to see how to do this. If you are using ANCOVA, you will also want to use hierarchical regression. See the section on ANOVA and ANCOVA.

4. If you have 3 or more IVs, you have to make some choices. The first choice is whether you want to use regression versus path analysis or structural equation modeling. If you have hypothesized causal chains, mediator variables, or partial correlations, you probably want to use path analysis or structural equation modeling rather than regression, although simple regression programs can do everything except structural equation modeling for you. If you have latent variables (factors or unobserved variables) in your model, use structural equation modeling. If you have no hypothetical cause and effect relations among your set of independent variables, you should probably analyze your data with multiple regression.

5. Use hierarchical regression when you have some a priori reason to order your variables. For example, suppose you have developed a new measure of anxiety and you want to demonstrate its merit. You might show that your new measure is good by comparing it to an existing, commonly used measure of anxiety. Suppose your DV is GSR (galvanic skin response), which is a measure of stress. You predict GSR using the old measure of anxiety and find R-square. You then add your new measure of anxiety to the equation to see if R-square increases significantly. If it does, then you have a strong argument that your new measure is worthwhile. Of course, if you just have the two anxiety measures and GSR, you have a simple correlation matrix. That and simultaneous regression are all that you need to tell the whole story. (What are the possible outcomes of the story?) But suppose you have developed a new multidimensional personality battery. We could use the old battery (say 3 variables) to predict a criterion of interest, and then add the new battery (3 variables) to see if R-square increases significantly. If it does, then we have an argument for the new battery.

6. The end result of a regression analysis is usually a simultaneous regression. That is, you report an analysis in which all of the variables of interest are entered into the regression equation at the same time. Report all b weights and the significance of each. The main drawback to this approach is that sometimes your IVs are (very) highly correlated and this results in poorly estimated and nonsignificant b weights. You need to check on this in your correlation matrix at the first step and also take a look at collinearity diagnostics (these are described under the section on Collinearity). If correlation among your IVs is a problem, there are several steps you might take to solve it.