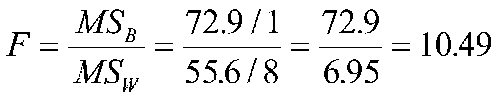
ANOVA 1
Objectives
What is the difference between a continuous variable and a categorical variable? Give a concrete example of each.
What is dummy [effect, orthogonal] coding?
What do the intercept and b weights mean for these models?
Why might I choose one model rather than another (that is, choose either dummy, effect or orthogonal coding) to analyze my data?
Is there any advantage to using regression rather than some ANOVA program to analyze designs with categorical IVs? What effect does unbalanced (unequal) cell size have on the interpretation of dummy [effect, orthogonal] coded regression slopes and intercepts?
| Orthogonal coding | Unequal Sample Sizes |
Categorical IVs: Dummy, Effect, & Orthogonal Coding
What we are doing here is ANOVA with regression techniques; that is, we are analyzing categorical (nominal) variables rather than continuous variables. There are some advantages to doing this, especially if you have unequal cell sizes. The computer will be doing the work for you. However, I want to show you what happens with the 3 kinds of coding so you will understand it. You are already familiar with ANOVA, so I am not going to discuss it. We are going to cover lots of ground quickly here. This is designed merely to familiarize you with the correspondence between regression and analysis of variance. Both methods are specific cases of a larger family called the general linear model.
With this kind of coding, we put a '1' to indicate that a person is a member of a category, and a '0' otherwise. Category membership is indicated in one or more columns of zeros and ones. For example, we could code sex as 1=female 0=male or 1=male 0=female. If we did, we would have a column variable indicating status as male or female. Or we could code for marital status as 1=single 0=married or 1=married 0=single. Ordinarily if we wanted to test for group differences, we would use a t-test or an F-test. But we can do the same thing with regression. Let's suppose we want to know whether people in general are happier if they are married or single. So we take a small sample of people shopping at University Square Mall and promise them some ice cream if they fill out our life satisfaction survey, which some do. They also fill out some demographic information, an item of which is marital status (Status), which we code 1=single 0=married. For fun, let's see what happens if we code it the other way (Status 2; 0=single 1=married) Our data:
|
|
Status |
Satisfaction |
Status2 |
|
|
|
|
Single |
1 |
25 |
0 |
|
|
|
|
S |
1 |
28 |
0 |
|
|
|
|
S |
1 |
20 |
0 |
|
|
|
|
S |
1 |
26 |
0 |
|
|
|
|
S |
1 |
25 |
0 |
M = 24.8 |
SD = 2.95 |
N=5 |
|
Married |
0 |
30 |
1 |
|
|
|
|
M |
0 |
28 |
1 |
|
|
|
|
M |
0 |
32 |
1 |
|
|
|
|
M |
0 |
33 |
1 |
|||
|
M |
0 |
28 |
1 |
M = 30.20 |
SD = 2.28 |
N=5 |
|
M |
.5 |
27.5 |
.5 |
|
|
|
|
SD |
.53 |
3.78 |
.53 |
|
|
|
|
Sat |
Grand mean |
Dev |
Dev2 |
Cell Mean |
Dev |
Dev2 |
|
25 |
27.5 |
-2.5 |
6.25 |
24.8 |
0.2 |
.04 |
|
28 |
27.5 |
0.5 |
0.25 |
24.8 |
3.2 |
10.24 |
|
20 |
27.5 |
-7.5 |
56.25 |
24.8 |
-4.8 |
23.04 |
|
26 |
27.5 |
-1.5 |
2.25 |
24.8 |
1.2 |
1.44 |
|
25 |
27.5 |
-2.5 |
6.25 |
24.8 |
0.2 |
.04 |
|
30 |
27.5 |
2.5 |
6.25 |
30.2 |
-.2 |
.04 |
|
28 |
27.5 |
0.5 |
0.25 |
30.2 |
-2.2 |
4.48 |
|
32 |
27.5 |
4.5 |
20.25 |
30.2 |
1.8 |
3.24 |
|
33 |
27.5 |
5.5 |
30.25 |
30.2 |
2.8 |
7.84 |
|
28 |
27.5 |
0.5 |
0.25 |
30.2 |
-2.2 |
4.84 |
|
Sum |
275 |
0 |
128.5 |
275 |
0 |
55.60 |
We have 10 people, 5 each in two groups. The sum of squared deviations from the grand mean is 128.5 (SStot); the sum of squared deviations from the cell means is 55.60 (SSwithin), and difference must be SSbetween = 128.5-55.60 = 72.90. To test for the difference we find the ratio of the two mean squares:
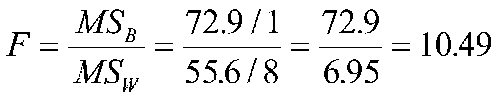
Or we could compute a t-test by
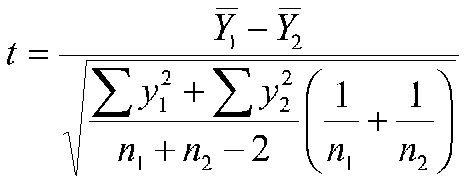
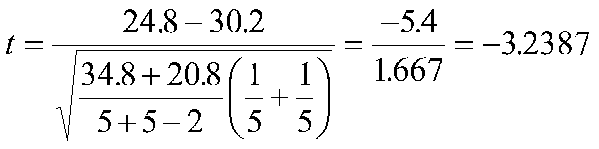
And if we square this result, we get 10.49, which is our value for F (recall that F = t2).
To compute regressions, we find that:
|
X |
Mean X |
x |
x2 |
Y |
Mean Y |
y |
xy |
|
1 |
0.5 |
0.5 |
0.25 |
25 |
27.5 |
-2.5 |
-1.25 |
|
1 |
0.5 |
0.5 |
0.25 |
28 |
27.5 |
0.5 |
0.25 |
|
1 |
0.5 |
0.5 |
0.25 |
20 |
27.5 |
-7.5 |
-3.75 |
|
1 |
0.5 |
0.5 |
0.25 |
26 |
27.5 |
-1.5 |
-0.75 |
|
1 |
0.5 |
0.5 |
0.25 |
25 |
27.5 |
-2.5 |
-1.25 |
|
0 |
0.5 |
-0.5 |
0.25 |
30 |
27.5 |
2.5 |
-1.25 |
|
0 |
0.5 |
-0.5 |
0.25 |
28 |
27.5 |
0.5 |
-0.25 |
|
0 |
0.5 |
-0.5 |
0.25 |
32 |
27.5 |
4.5 |
-2.25 |
|
0 |
0.5 |
-0.5 |
0.25 |
33 |
27.5 |
5.5 |
-2.75 |
|
0 |
0.5 |
-0.5 |
0.25 |
28 |
27.5 |
0.5 |
-0.25 |
|
Sums |
|||||||
|
5 |
5 |
0 |
2.5 |
275 |
275 |
0 |
-13.5 |
|
Formula |
Status |
Status2 |
|
|
-13.5/2.5 = -5.4 |
13.5/2.5 = 5.4 |
|
|
27.5-(-5.4*.5)= 30.20 |
27.5-(5.4*.5) = 24.8 |
|
|
Y' =30.20-5.4X |
Y'=24.8+5.4X |
|
|
-5.4(-13.5)=72.90 |
5.4(13.5)=72.90 |
|
|
128.5-72.90=55.6 |
128.5-72.9=55.6 |
|
|
55.6/8 = 6.95 |
55.6/8=6.95 |
|
|
Sqrt(6.95/2.5) = 1.667 |
Sqrt(6.95/2.5) = 1.667 |
|
|
-5.4/1.667 = -3.239 |
5.4/1.667 = 3.239 |
|
|
72.9/128.5=.5673 |
72.9/128.5=.5673 |
|
|
(.57/1)/(.43/8)= 10.49 |
(.57/1)/(.43/8)= 10.49 |
Points to notice:
We can apply dummy coding to categorical variables with more than two levels. We can keep the use of zeros and ones as well. However, we will always need as many columns as there are degrees of freedom. With two levels, we need one column; with three levels, we need two columns. With C levels, we need C-1 columns.
Suppose we have three groups of people, single, married, and divorced, and we want to estimate their life satisfaction. Note how the first vector selects (identifies) the single group, and the second identifies the married group. The divorced folks are left over. The overall results will be the same, however, no matter which groups we select.
|
Group |
Satis-faction |
Vector1 |
Vector2 |
Satis Group Mean |
|
Single |
25 |
1 |
0 |
24.80 |
|
S |
28 |
1 |
0 |
|
|
S |
20 |
1 |
0 |
|
|
S |
26 |
1 |
0 |
|
|
S |
25 |
1 |
0 |
|
|
Married |
30 |
0 |
1 |
30.20 |
|
M |
28 |
0 |
1 |
|
|
M |
32 |
0 |
1 |
|
|
M |
33 |
0 |
1 |
|
|
M |
28 |
0 |
1 |
|
|
Divorced |
20 |
0 |
0 |
23.80 |
|
D |
22 |
0 |
0 |
|
|
D |
28 |
0 |
0 |
|
|
D |
25 |
0 |
0 |
|
|
D |
24 |
0 |
0 |
|
|
Grand Mean |
26.27 |
.33 |
.33 |
|
The descriptive statistics for the variables are:
|
|
Sat |
V1 |
V2 |
|
Satisfaction |
1 |
|
|
|
Vector 1 |
-.28 |
1 |
|
|
Vector 2 |
.74 |
-.50 |
1 |
|
Mean |
26.27 |
.33 |
.33 |
|
SD |
3.88 |
.49 |
.49 |
When we run the program with satisfaction as the DV and the two vectors as the IVs, we find that R2 is .5619. The significance of this is found by:
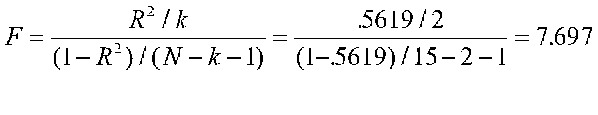
Note that there are three groups and thus two degrees of freedom between groups. There are 15 people and thus 12 df for error. The F test based on R2 gives us the same result we would get if we used the traditional ANOVA approach to analyze these data.
The parameter estimates for these data are:
|
Variable |
df |
Est |
Std Err |
t |
P > |t| |
|
Intercept |
|
23.8 |
1.24 |
19.18 |
.0001 |
|
V1 |
1 |
1 |
1.75 |
.57 |
.5793 |
|
V2 |
1 |
6.4 |
1.75 |
3.65 |
.0033 |
Thus, the regression equation using this particular dummy code is:
Y' = 23.8 + 1(V1) + 6.4(V2)
Points to notice:
The group that gets all zeros is the base group or comparison group. The regression coefficients present a contrast or difference between the group identified by the vector and the base or comparison group. For our example, the comparison group is the divorced group. The first b weight corresponds to the single group and the b represents the difference between the means of the divorced and single groups. The second b weight represents the difference in means between the divorced and married groups.
The tests of significance of the b weights are equivalent to t-tests of the difference between the means of the identified and comparison groups.
Effect coding is similar to dummy coding. The difference in coding is that, in effect coding, the comparison group is identified by the symbol -1. Our example looks like this:
|
Group |
Satisfaction |
Vector1 |
Vector2 |
Satis Group Mean |
|||
|
Single |
25 |
1 |
0 |
24.80 |
|||
|
S |
28 |
1 |
0 |
|
|||
|
S |
20 |
1 |
0 |
|
|||
|
S |
26 |
1 |
0 |
|
|||
|
S |
25 |
1 |
0 |
|
|||
|
Married |
30 |
0 |
1 |
30.20 |
|||
|
M |
28 |
0 |
1 |
|
|||
|
M |
32 |
0 |
1 |
|
|||
|
M |
33 |
0 |
1 |
||||
|
M |
28 |
0 |
1 |
|
|||
|
Divorced |
20 |
-1 |
-1 |
23.80 |
|||
|
D |
22 |
-1 |
-1 |
|
|||
|
D |
28 |
-1 |
-1 |
|
|||
|
D |
25 |
-1 |
-1 |
|
|||
|
D |
24 |
-1 |
-1 |
|
|||
|
Grand Mean |
26.27 |
0 |
0 |
|
|||
|
|
|
|
|
|
|||
|
Descriptives |
Sat |
V1 |
V2 |
||||
|
Satisfaction |
1 |
|
|
||||
|
Vector 1 |
.11 |
1 |
|
||||
|
Vector 2 |
.70 |
.50 |
1 |
||||
|
Mean |
26.27 |
.0 |
.0 |
||||
|
SD |
3.88 |
.85 |
.85 |
||||
The R2 for this model is also .5619. The estimates are somewhat different, however.
|
Variable |
Df |
Est |
Std Err |
t |
P > |t| |
|
Intercept |
|
26.27 |
.72 |
36.66 |
.0001 |
|
V1 |
1 |
-1.47 |
1.01 |
-1.45 |
.17 |
|
V2 |
1 |
3.93 |
1.01 |
3.88 |
.002 |
Note that regression equation is different.
Y' = 26.27 -1.47(V1)+3.93(V2)
Points to notice:
Orthogonal coding is used to compute contrasts. You can use it if you have specific planned comparisons going into the analysis. Our example:
|
Group |
Satisfaction |
Vector1 |
Vector2 |
Satis Mean |
|||
|
Single |
25 |
-1 |
1 |
24.80 |
|||
|
S |
28 |
-1 |
1 |
|
|||
|
S |
20 |
-1 |
1 |
|
|||
|
S |
26 |
-1 |
1 |
|
|||
|
S |
25 |
-1 |
1 |
|
|||
|
Married |
30 |
1 |
1 |
30.20 |
|||
|
M |
28 |
1 |
1 |
|
|||
|
M |
32 |
1 |
1 |
|
|||
|
M |
33 |
1 |
1 |
||||
|
M |
28 |
1 |
1 |
|
|||
|
Divorced |
20 |
0 |
-2 |
23.80 |
|||
|
D |
22 |
0 |
-2 |
|
|||
|
D |
28 |
0 |
-2 |
|
|||
|
D |
25 |
0 |
-2 |
|
|||
|
D |
24 |
0 |
-2 |
|
|||
|
Grand Mean |
26.27 |
0 |
0 |
|
|||
|
Descriptives |
Sat |
V1 |
V2 |
||||
|
Satisfaction |
1 |
|
|
||||
|
Vector 1 |
.59 |
1 |
|
||||
|
Vector 2 |
.47 |
.00 |
1 |
||||
|
Mean |
26.27 |
0.0 |
0.0 |
||||
|
SD |
3.88 |
.85 |
1.46 |
||||
Take a look at the contrasts implied by the positive and negative numbers in the two vectors. In the first vector, we are comparing single and married people; we are ignoring divorced people. In the second vector, we are comparing the mean of both single and married people to the mean of the divorced group. Notice in the correlation matrix that V1 and V2 are not correlated, hence orthogonal coding. There are only as many orthogonal contrasts allowed in one analysis as there are degrees of freedom. In this case, there are two. Exactly which two are tested depends entirely upon the design and hypothesized effects. In our example, we would need to specify in advance that we expect differences between single and married and between both these and divorced. We could have chosen other contrasts -- we could have hypothesized that the single would be different from the combined married and divorced, for example.
The R2 for this analysis is .5619, just as for dummy and effect coding.
|
Variable |
df |
Est |
Std Err |
t |
P > |t| |
|
Intercept |
|
26.27 |
.72 |
36.66 |
.0001 |
|
V1 |
1 |
2.70 |
.88 |
3.08 |
.01 |
|
V2 |
1 |
1.23 |
.51 |
2.43 |
.03 |
Points to notice:
Y' = 26.27 + 2.70(-1) + 1.23(1).
People in the divorced group have predicted scores of
Y' = 26.27 + 2.70(0) + 1.23(-2).
Designs in which the cells contain unequal frequencies introduce minor complications to the types of coding shown here. For effect coding, the meaning of the intercept changes. For effect coding, the intercept will no longer refer to the grand mean. Instead, it will denote the unweighted mean of the cell means.
That is, instead of
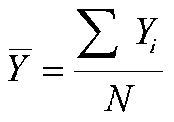
where Yi is the individual scores on the DV, we have, say,
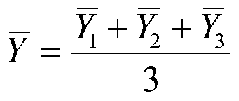
with three cells. Note that the results will not be the same if the cells do not have equal frequencies. In the case of equal frequencies, both values of mean Y, weighted and unweighted, are the same. With orthogonal coding, the intercept will still be the grand mean, but we have to change the values of the codes to maintain orthogonality. For dummy coding, the intercept still refers to the mean of the base or comparison group.
For orthogonal coding, you have to adjust the code numbers to keep the sums equal to zero and the vectors orthogonal. For example,
|
Group |
Satisfaction |
Vector1 |
Vector2 |
Satis Group Mean |
|
Single |
25 |
-4 |
5 |
24.33 |
|
S |
28 |
-4 |
5 |
|
|
S |
20 |
-4 |
5 |
|
|
Married |
30 |
3 |
5 |
30.75 |
|
M |
32 |
3 |
5 |
|
|
M |
33 |
3 |
5 |
|
|
M |
28 |
3 |
5 |
|
|
Divorced |
20 |
0 |
-7 |
23.80 |
|
D |
22 |
0 |
-7 |
|
|
D |
28 |
0 |
-7 |
|
|
D |
25 |
0 |
-7 |
|
|
D |
24 |
0 |
-7 |
|
|
M |
26.27 |
0 |
0 |
|
The correlation between V1 and V2 is still zero.
Otherwise, the results of the regressions are the same. All three types of codings give the same R2. The interpretation of the b weights is what it was before (for dummy coding, the contrast between a cell and a comparison cell, for effect, the contrast between a cell and the (unweighted) mean, and for orthogonal, specific planned comparisons.